Short talk proposals
Procedure available in pdf format.
The afternoons of the Journées will be devoted to short talks of 20 minutes in parallel sessions. There will be a significant number of talks (approximately 200). However, the number of proposals may be higher than possible or the quality of certain proposals may not be sufficient for the scientific level of the conference. The JA2017 Scientific Committee will then decide.
To submit an abstract, please follow the following procedure carefully:
- Register for the conference (you don't need to pay at this step). No proposal from a non-registered people will be considered.
- Send a message to Bruno Deschamps : xxx.yyy@univ-lemans.fr where xxx.yyy=bruno.deschamps entilted "Expose JA2017".
- Attach to this message the LaTeX source file of the proposal. This file must contain only the following fields, filled in:
\titres{Short title}{Full Title} \auteur{First name}{Last name} \universite{Affiliation} \resume{Abstract of the talk} \mel{email}The name of the file must correspond to the name of the author (see example below). - Attach to this message the pdf file of the abstract.
- Indicate in your message the list of packages useful for compilation (and only them).No personal macrowill be taken into account, please write your abstract using only the usual LaTeX macros.
-
- You will receive a response few days later. In case of acceptance, you will have to pay fee as soon as possible.
- If you need one, you can ask for an invitation letter mentionning that your talk has been accepted. Just send a message to xxx.yyy@univ-lemans.fr where xxx.yyy=bruno.deschamps entilted "Lettre JA2017".
The deadline for submission is April 26, 2017
Example :
Pierre de Fermat wants to propose the following abstract:
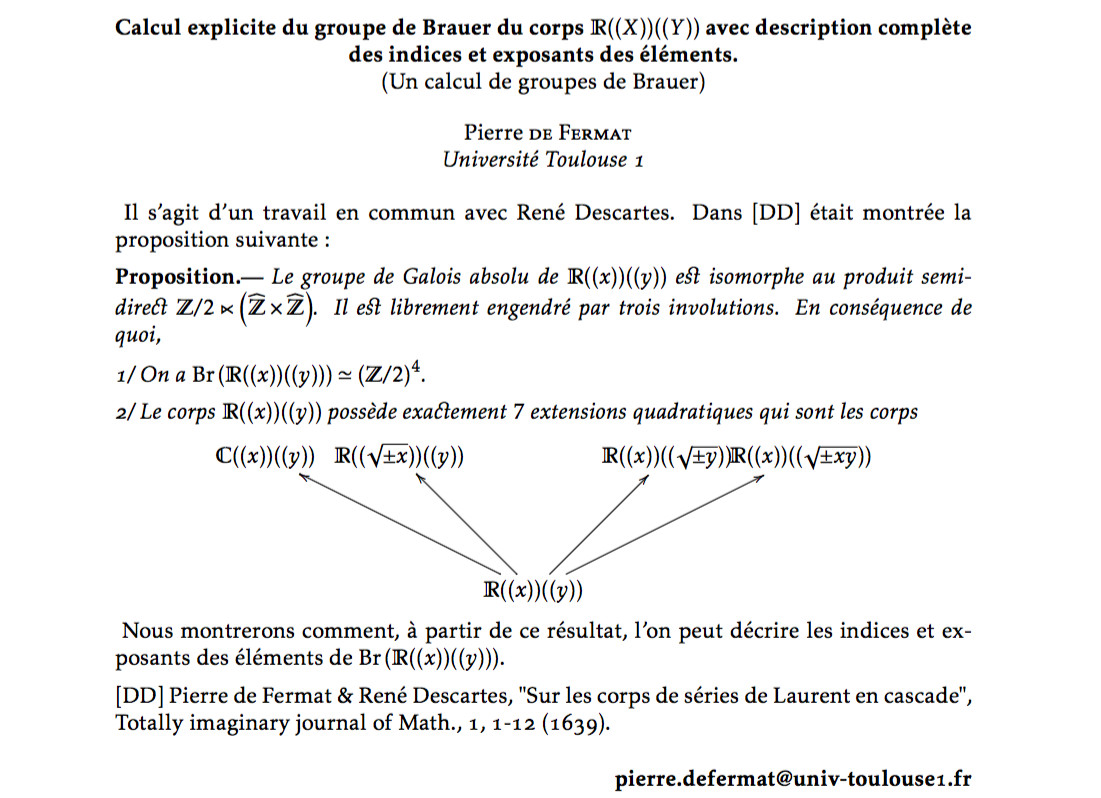
He sends as an attachment the following file named defermat.tex:
\titres{Un calcul de groupes de Brauer}{Calcul explicite du groupe de Brauer du corps
${\mathbb R}((X))((Y))$ avec description complète des indices et exposants des éléments.}
\auteur{Pierre}{de Fermat}
\universite{Université Toulouse 1}
\resume{Il s'agit d'un travail en commun avec René Descartes.
Dans [DD] était montrée la proposition suivante :
\vskip 2mm
\noindent
{\bf Proposition.---} {\it Le groupe de Galois absolu de ${\mathbb R}((x))((y))$ est isomorphe au
produit semi-direct
$\displaystyle {\mathbb Z}/2 \ltimes \left(\widehat{\mathbb Z}\times \widehat{\mathbb Z}\right)$.
Il est librement engendré par trois involutions. En conséquence de quoi,
\vskip 2mm
\noindent
1/ On a
$\displaystyle \hbox{\rm Br}\left({\mathbb R}((x))((y))\right)\simeq\left({\mathbb Z}/2\right)^4$.
\vskip 2mm
\noindent
2/ Le corps ${\mathbb R}((x))((y))$ possède exactement $7$ extensions quadratiques
qui sont les corps
\vskip 2mm
\noindent
$$\xymatrix @!0 @R=6em @C=6pc{ {\mathbb C}((x))((y))&
{\mathbb R}((\sqrt{\pm x}))((y))&&{\mathbb R}((x))((\sqrt{\pm y}))&
{\mathbb R}((x))((\sqrt{\pm xy}))\\
&&{\mathbb R}((x))((y)) \ar[rru]\ar[ru]\ar[llu]\ar[lu]&&\\
}$$}
Nous montrerons comment, à partir de ce résultat, l'on peut décrire les indices et exposants
des éléments de $\hbox{\rm Br}\left({\mathbb R}((x))((y))\right)$.
\vskip 2mm
\noindent
[DD] Pierre de Fermat \& René Descartes, "Sur les corps de séries de Laurent en cascade",
Totally imaginary journal of Math., 1, 1-12 (1539).}
\mel{pierre.defermat@univ-toulouse1.fr}
and he writes in his email message:
\usepackage[T1]{fontenc}
\usepackage[all]{xy}